已知△ABC的面积S满足
(Ⅰ)求θ的取值范围;
(Ⅱ)求函数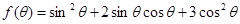 的最大值。
的最大值。
如图,在圆 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.设
为垂足.设 为线段
为线段 的中点.
的中点.
(1)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(2)若圆 在点
在点 处的切线与
处的切线与 轴交于点
轴交于点 ,试判断直线
,试判断直线 与轨迹
与轨迹 的位置关系.
的位置关系.
已知函数 (
( ,
, ,
, ),
), 的部分图像如图所示,
的部分图像如图所示, 、
、 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点 的坐标为
的坐标为 .
.
(1)求 的最小正周期及
的最小正周期及 的值;
的值;
(2)若点 的坐标为
的坐标为 ,
, ,求
,求 的值和
的值和 的面积.
的面积.
下图是预测到的某地5月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天
(1)求此人到达当日空气质量优良的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明).
已知函数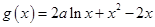 .
.
(1)当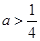 时,讨论函数
时,讨论函数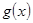 的单调性;
的单调性;
(2)当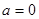 时,在函数
时,在函数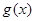 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为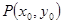 ,试探究函数
,试探究函数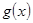 在Q
在Q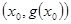 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?
(3)试判断当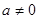 时
时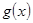 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.
已知椭圆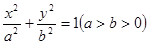 的离心率为
的离心率为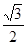 ,点
,点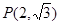 在椭圆上.
在椭圆上.
(1)求椭圆C的方程;
(2)设椭圆的左右顶点分别是A、B,过点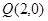 的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.