已知函数f(x)=sin 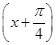 ·sin
·sin  +
+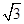 sin xcos x(x∈R).
sin xcos x(x∈R).
(1)求f 的值;
的值;
(2)在△ABC中,若f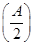 =1,求sin B+sin C的最大值.
=1,求sin B+sin C的最大值.
若集合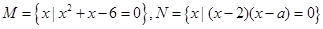 ,且
,且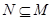 ,求实数
,求实数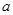 的值;
的值;
本小题满分13分)
已知圆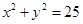 ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
(Ⅰ)若△ABC的重心是G(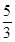 ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程;
(Ⅱ)若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值.
(本小题满分13分)
已知直线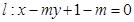
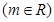 ,圆
,圆 .
.
(Ⅰ)证明:对任意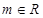 ,直线
,直线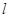 恒过一定点N,且直线
恒过一定点N,且直线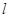 与圆C恒有两个公共点;
与圆C恒有两个公共点;
(Ⅱ)设以CN为直径的圆为圆D(D为CN中点),求证圆D的方程为: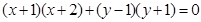
(Ⅲ)设直线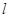 与圆
与圆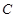 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: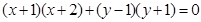 交于点
交于点 (异于C、N),当
(异于C、N),当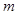 变化时,求证
变化时,求证 为AB的中点.
为AB的中点.
(本小题满分13分)
如图,在直三棱柱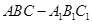 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中, 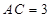 ,
,  ,
,  ,
, 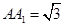 ,点
,点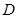 是
是 的中点.
的中点. 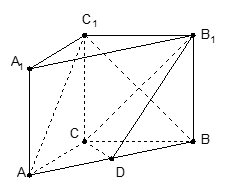
(Ⅰ) 求证: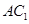 ∥平面
∥平面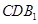 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.
(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.