在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1).设k为非零实数,矩阵M=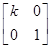 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.
(本小题满分12分)
已知数列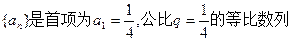 ,设
,设 ,数列
,数列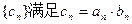 。(1)求证:
。(1)求证: 是等差数列; (2)求数列
是等差数列; (2)求数列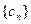 的前n项和Sn;
的前n项和Sn;
(3)若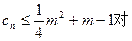 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
(本小题满分12分)
某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交 元(
元( 为常数,
为常数,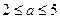 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与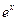 (
( 为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润
为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润 元与每件产品的日售价
元与每件产品的日售价 元的函数关系式;当每件产品的日售价为多少元时该商店的日利润
元的函数关系式;当每件产品的日售价为多少元时该商店的日利润 最大,说明理由。
最大,说明理由。
如图,已知四棱锥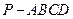 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面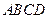 ,且
,且 ,点
,点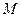 、
、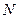 分别在侧棱
分别在侧棱 、
、 上,且
上,且

(Ⅰ)求证: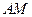 ⊥平面
⊥平面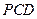 ;
;
(Ⅱ)若 ,求平面
,求平面 与平面
与平面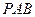 的所成锐二面角的大小
的所成锐二面角的大小
(本小题满分12分)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(Ⅰ)确定角C的大小:(Ⅱ)若c=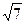 ,且△ABC的面积为
,且△ABC的面积为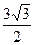
 ,求a+b的值。
,求a+b的值。
(本小题满分14分) 已知函数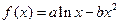 图象上一点
图象上一点 处的切线方程为
处的切线方程为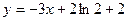 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程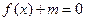 在
在 内有两个不等实根,求
内有两个不等实根,求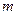 的取值范围(其中
的取值范围(其中 为自然对数的底数);(Ⅲ)令
为自然对数的底数);(Ⅲ)令 ,若
,若 的图象与
的图象与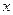 轴交于
轴交于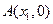 ,
,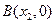 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 在
在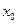 处的导数
处的导数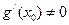 .
.