已知向量p＝(an，2n)，q＝(2n＋1，－an＋1)，n∈N*，p与q垂直，且a1＝1.
(1)求数列{an}的通项公式；
(2)若数列{bn}满足bn＝log2an＋1，求数列{an·bn}的前n项和Sn.
（本小题满分12分）已知
，
（1）求
及
；
（2）求
的值．
计算以下式子的值：
（1）
；
（2）
．
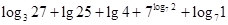已知函数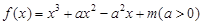
．
若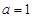
时函数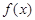
有三个互不相同的零点，求实数
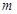的取值范围；
若对任意的
，不等式
对任意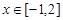
恒成立，求实数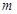的取值范围．
已知椭圆C的中心在原点，焦点在坐标轴上，短轴的一个端点B（0，4），离心率e=0．6．
（1）求椭圆C的方程；
（2）若O（0，0），P（2，2），试探究在椭圆C内部是否存在整点Q（平面内横、纵坐标都是
整数的点为整点），使得△OPQ的面积S△OPQ=4?若存在，请指出共有几个这样的点（不必具体求出这些点的坐标）；否则，说明理由．
已知等比数列{
}的前
项和为
，且满足
．
（1）求
的值及数列{}的通项公式；
（2）若数列{
}满足
,求数列{}的前和
．