今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:
| A.非常了解; | B.比较了解; | C.基本了解; | D.不了解.根据调查统计结果,绘制了下面的三种统计图表. |
请结合统计图表,回答下列问题.
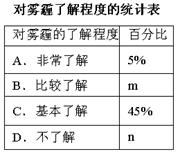
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全图1所示的条形统计图;
解方程
(1)2(3-x)=-4x+5
(2)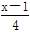 =
=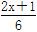 +1
+1
阅读:如图1,在△ABC中,3∠ A+∠ B=180°,BC=8,AC=10,求AB的长.
小明的思路:如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,易得∠A=∠D,△ABD为等腰三角形,由3∠A+∠B=180°和∠A+∠ABC+∠BCA=180°,易得∠BCA=2∠A,△BCD为等腰三角形,依据已知条件可得AE和AB的长.
解决下列问题:
(1)图2中,AE= ,AB= ;
(2)在△ABC中,∠A,∠B,∠C的对边分别为a、b、c.如图3,当3∠A+2∠B=180°时,用含a,c式子表示b.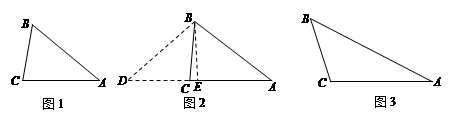
如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.现将线段AC沿AD折叠后,使得点C落在AB上,求折痕AD的长度.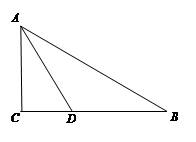
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠ A的度数.