某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照
，
，
，
，
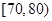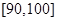的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在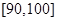，的数据）
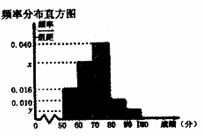
（1）求样本容量n和频率分布直方图中x，y的值；
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设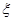
表示所抽取的3名同学中得分在的学生个数，求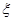的分布列及其数学期望
时，求证：
,当
时,
的极大值为7;当
时,
的值； (2)函数
在(0,6)上的单调区间。
过点(2, 8)的切线方程；
过点（0，0）的切线方程。