已知函数


 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的斜率为
处的切线的斜率为 ,问:
,问:  在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个 ,使得
,使得 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.
求直线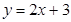 与抛物线
与抛物线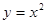 所围成的图形面积是。
所围成的图形面积是。
求f(x)= 在区间
在区间 上的最值。
上的最值。
已知数列 的前
的前 项和为
项和为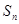 ,
,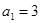 且
且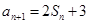 ,数列
,数列 为等差数列,且公差
为等差数列,且公差 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 成等比数列,求数列
成等比数列,求数列 的前项和
的前项和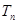
某商店预备在一个月内分批购入每张价值为20元的书桌共36台,每批都购入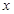 台(
台(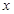 是正整数),且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
是正整数),且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
(1)求该月需用去的运费和保管费的总费用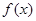
(2)能否恰当地安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
如图,在三棱柱 中,底面
中,底面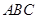 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱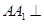 面
面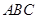 ,点
,点 是
是 的中点.
的中点.
(1)求证: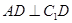 ;
;
(2)求三棱锥 的体积;
的体积;
(3)求证: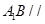 平面
平面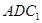 .
.