如图,直线AB过圆心O,交 于F(不与B重合),直线
于F(不与B重合),直线 与
与 相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
求证:(1) ;(2)
;(2) .
.
⑴在 中,已知
中,已知 求此三角形最小边的长;
求此三角形最小边的长; ⑵在
⑵在 中
中 ,已知
,已知 ,求
,求 .
.

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图 .
⑴根据茎叶图判断哪个班的平均身高较高;
⑵计算甲班的样本方差.
(本小题满分14分:6+8)
某投资公司投资甲、乙两个项目所得的利润分别是 P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式
P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
(1)求y关于x的函数表达式;
(2)求总利润的最大值。
(本小题满分16分:4+5 +7)
+7)
已知函数 ,其中e为常数,
,其中e为常数,
(e=2.71828...),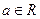
(1)当a=1时,求 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,
(3)是否存在实数 ,使
,使 最小值为3,若存在,求出
最小值为3,若存在,求出 的值,若不存在,说明理由。
的值,若不存在,说明理由。
(本小题满分16分:8+8) 19
19
给出函数封闭的定义:若对于定义域D内的任一个自变量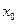 ,都有函数值
,都有函数值 ,则称函数y=f(x)
,则称函数y=f(x) 在 D上封闭。
在 D上封闭。
(1)若定义域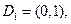 判断下列函数中哪些在
判断下列函数中哪些在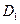 上封闭,并给出推理过程;
上封闭,并给出推理过程;
(2)若定义域 是否存在实数
是否存在实数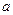 ,使函数
,使函数 在
在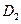 上封闭,若存在,求出
上封闭,若存在,求出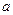 值,若不存在,请说明理由。
值,若不存在,请说明理由。