本小题满分12分）
在直三棱柱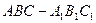
中， AC=4,CB=2,AA1=2
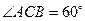，E、F分别是
的中点。
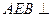（1）证明：平面
平面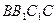
；
（2）证明：
平面ABE；
(3)设P是BE的中点，求三棱锥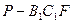
的体积。
已知函数
（Ⅰ）若
，求函数
的极小值；
（Ⅱ）设函数
，试问：在定义域内是否存在三个不同的自变量
使得
的值相等，若存在，请求出
的范围，若不存在，请说明理由？
如图，在矩形
中，
分别为四边的中点，且都在坐标轴上，设
,
．
（Ⅰ）求直线
与
的交点
的轨迹
的方程；
（Ⅱ）过圆
上一点
作圆的切线与轨迹交于
两点，若
，试求出
的值．
如图，在三棱锥
中，
，
，设顶点
在底面
上的射影为
．
（Ⅰ）求证:
；
（Ⅱ）设点
在棱
上，且
，试求二面角
的余弦值．
现有4个人去参加春节联欢活动，该活动有甲、乙两个项目可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢，掷出点数为1或2的人去参加甲项目联欢，掷出点数大于2的人去参加乙项目联欢.
（Ⅰ）求这4个人中恰好有2人去参加甲项目联欢的概率；
（Ⅱ）求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率；
（Ⅲ）用
分别表示这4个人中去参加甲、乙项目联欢的人数，记
，求随机变量
的分布列与数学期望
.
如图，在
中，
，垂足为
，且
． 
（Ⅰ）求
的大小；
（Ⅱ）设
为
的中点，已知的面积为15，求
的长．