如图所示,已知平面α∥平面β,点P是平面α、β外一点,且直线PB分别与α、β相交于A、B,直线PD分别与α、β相交于C、D.
(1)求证:AC∥BD;
(2)如果PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.
如图,四棱柱 中,
中,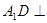 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 .
.
(1)求三棱锥 的体积;
的体积;
(2)求直线 与平面
与平面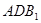 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一点
上存在一点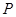 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
已知数列 的各项均为正数,前
的各项均为正数,前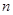 项和为
项和为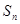 ,且
,且
(1)求证数列 是等差数列;
是等差数列;
(2)设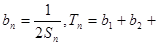 …
… ,求
,求 。
。
选修4-5:不等式选讲
已知关于 的不等式:
的不等式: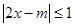 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(1)求整数 的值;(2)在(1)的条件下,解不等式:
的值;(2)在(1)的条件下,解不等式: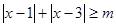 .
.
选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是 ,曲线
,曲线 的参数方程是
的参数方程是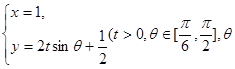 是参数).
是参数).
(1)写出曲线 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;
(2)求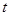 的取值范围,使得
的取值范围,使得 ,
, 没有公共点.
没有公共点.
选修4-1:几何证明选讲
如图所示,已知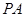 与⊙
与⊙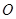 相切,
相切,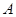 为切点,
为切点, 为割线,弦
为割线,弦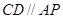 ,
, 、
、 相交于
相交于 点,
点, 为
为 上一点,且
上一点,且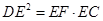
(1)求证: ;
;
(2)(2)求证: ·
· =
= ·
· .
.