(拓展深化)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α.且DM交AC于F,ME交BC于G,
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连接FG,如果α=45°,AB=4 ,AF=3,求FG的长.
,AF=3,求FG的长.
已知函数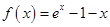
(1)求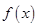 的最小值;
的最小值;
(2)设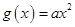 ,
, .
.
(ⅰ)证明:当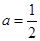 时,
时,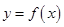 的图象与
的图象与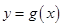 的图象有唯一的公共点;
的图象有唯一的公共点;
(ⅱ)若当 时,
时,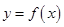 的图象恒在
的图象恒在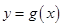 的图象的上方,求实数
的图象的上方,求实数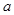 的取值范围.
的取值范围.
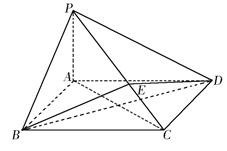
如图所示,在四棱锥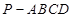 中,底面
中,底面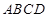 为矩形,
为矩形,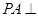 平面
平面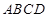 ,点
,点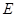 在线段
在线段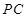 上,
上,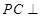 平面
平面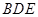 .
.
(1)证明: 平面
平面 .;
.;
(2)若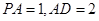 ,求三棱锥
,求三棱锥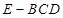 的体积.
的体积.
已知数列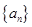 满足
满足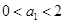 ,
,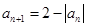 ,
,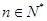 .
.
(1)若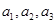 成等比数列,求
成等比数列,求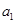 的值;
的值;
(2)是否存在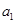 ,使数列
,使数列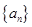 为等差数列?若存在,求出所有这样的
为等差数列?若存在,求出所有这样的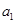 ;若不存在,说明理由.
;若不存在,说明理由.
在锐角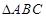 中,角
中,角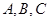 的对边分别为
的对边分别为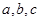 .已知
.已知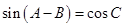 .
.
(1)求B;
(2)若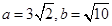 ,求
,求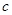 .
.
(1)已知函数f(x)=ex-1-tx,∃x0∈R,使f(x0)≤0,求实数t的取值范围;
(2)证明: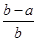 <ln
<ln <
<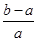 ,其中0<a<b;
,其中0<a<b;
(3)设[x]表示不超过x的最大整数,证明:[ln(1+n)]≤[1+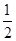 + +
+ +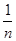 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).