如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.
(1)求直角三角形的三边长;
(2)求两直角边在斜边上的射影的长.
甲、乙两位同学从 共四所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学甲特别喜欢
共四所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学甲特别喜欢 高校,他除选
高校,他除选 高校外,再会在余下的3所中随机选1所;同学乙对4所高校没有偏爱,在4所高校中随机选2所.
高校外,再会在余下的3所中随机选1所;同学乙对4所高校没有偏爱,在4所高校中随机选2所.
(1)求乙同学选中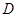 高校的概率;
高校的概率;
(2)求甲、乙两名同学恰有一人选中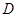 高校的概率.
高校的概率.
已知数列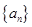 的前
的前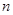 项和为
项和为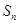 ,且
,且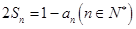 .
.
(1)求数列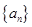 的通项公式;
的通项公式;
(2)设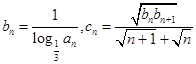 ,求数列
,求数列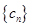 的前
的前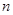 项和
项和 .
.
选修4-5:不等式选讲
已知函数 .
.
(1)当a=2时,解不等式 ;
;
(2)若存在实数x,使得不等式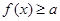 成立,求实数a的取值范围.
成立,求实数a的取值范围.
选修4-4:坐标系与参数方程
直线 (t为参数),圆
(t为参数),圆 (极轴与x轴的非负半轴重合,且单位长度相同).
(极轴与x轴的非负半轴重合,且单位长度相同).
(1)求圆心C到直线l的距离;
(2)若直线l被圆C截的弦长为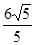 ,求a的值.
,求a的值.
选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP⊥OM于P.
(1)证明: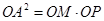 ;
;
(2)N为线段AP上一点,直线NB⊥ON且交圆O于B点,过B点的切线交直线ON于K.证明:∠OKM=90°.