如图,在四棱锥PABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=90°,且AB=2AD=2DC=2PD=4,E为PA的中点.
(1)求证:DE∥平面PBC;
(2)求证:DE⊥平面PAB.
已知椭圆C的焦点分别为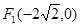 和
和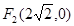 ,长轴长为6,设直线
,长轴长为6,设直线 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。
已知命题p:方程x2 + mx + 1=0有两个不相等的实根;q:不等式4x 2+4(m –2)x+1>0的解集为R;若p或q为真,p且q为假,求实数m的取值范围。
(本题12分)已知圆心为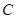 的圆经过点
的圆经过点 和
和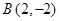 ,且圆心
,且圆心 在直线
在直线 上
上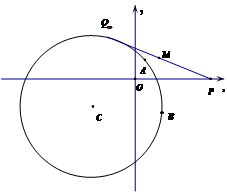
(1)求圆心为 的圆的标准方程;
的圆的标准方程;
(2)线段 的端点
的端点 的坐标是
的坐标是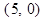 ,端点
,端点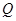 在圆
在圆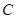 上运动,求线段
上运动,求线段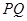 中点
中点 的轨迹方程.
的轨迹方程.
(本题12分)如图,边长为2的正方形 所在的平面与平面
所在的平面与平面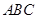 垂直,
垂直, 与
与 的交点为
的交点为 ,
,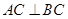 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面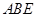 所成线面角的正切值.
所成线面角的正切值.
(本题10分)如图,三棱柱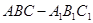 中,侧棱
中,侧棱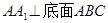 ,且侧棱和底面边长均为2,
,且侧棱和底面边长均为2, 是
是 的中点.
的中点.
(1)求证: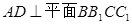 ;
;
(2)求证: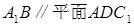 ;
;