如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.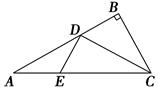
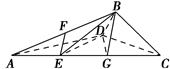
图1 图2
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.
(本小题共10分)
已知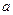 、
、 ,求证:
,求证: .
.
已知向量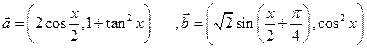 ,
,
(1)求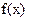 在
在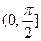 上的单调增区间;
上的单调增区间;
(2)若 ,求
,求 的值
的值
为了了解高中新生的体能情况,某学校抽取部分高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12﹒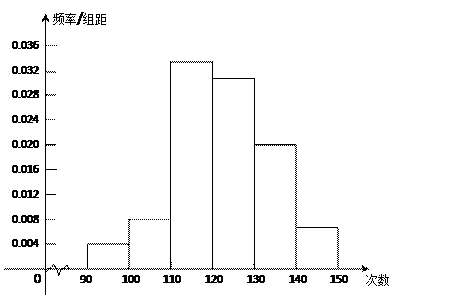
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(Ⅲ)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
在一个盒子中装有6支圆珠笔,其中3支一等品,2支二等品和1支三等品,从中任取3支﹒求
(Ⅰ)恰有1支一等品的概率;
(Ⅱ)没有三等品的概率﹒
(本题满分12分)已知 ,求
,求 的值。
的值。