为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
[70,80] |
| 人数 |
5 |
25 |
30 |
25 |
15 |
表2:女生上网时间与频数分布表
| 上网时间(分钟) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
[70,80] |
| 人数 |
10 |
20 |
40 |
20 |
10 |
(1)从这100名男生中任意选出3人,求其中恰有1人上网时间少于60分钟的概率;
(2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
| |
上网时间少于60分钟 |
上网时间不少于60分钟 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
|
附:K2=
| P(K2≥k0) |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
抛掷甲,乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体,其底面落于桌面,记底面上所得的数字分别为x,y.记 表示
表示 的整数部分,如:
的整数部分,如: ,设
,设 为随机变量,
为随机变量,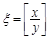 .
.
(Ⅰ)求概率 ;
;
(Ⅱ)求 的分布列,并求其数学期望
的分布列,并求其数学期望 .
.
在极坐标系中,直线 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为
,以极点为原点,极轴为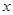 轴的正半轴建立平面直角坐标系,曲线
轴的正半轴建立平面直角坐标系,曲线 的参数方程为
的参数方程为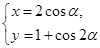 (
(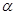 为参数),求直线
为参数),求直线 与曲线
与曲线 的交点P的直角坐标.
的交点P的直角坐标.
已知矩阵A=,若矩阵A属于特征值6的一个特征向量为α1=,属于特征值1的一个特征向
量为α2=.求矩阵A,并写出A的逆矩阵.
已知数列 为等差数列,
为等差数列, ,
, 的前
的前 和为
和为 ,数列
,数列 为等
为等
比数列,且 对任意的
对任意的 恒成立.
恒成立.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)是否存在非零整数 ,使不等式
,使不等式 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)各项均为正整数的无穷等差数列 ,满足
,满足 ,且存在正整数k,使
,且存在正整数k,使 成等比数列,若数列
成等比数列,若数列 的公差为d,求d的所有可能取值之和.
的公差为d,求d的所有可能取值之和.
设函数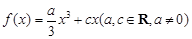 .
.
(Ⅰ)若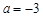 ,函数
,函数 在
在 的值域为
的值域为 ,求函数
,求函数 的零点;
的零点;
(Ⅱ)若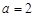 ,
,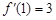 ,
, .
.
(1)对任意的 ,
, 恒成立, 求实数
恒成立, 求实数 的最小值;
的最小值;
(2)令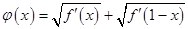 ,若存在
,若存在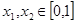 使得
使得 ,求实数
,求实数 的取值范围.
的取值范围.