某校高一年级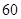 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下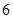 段:
段:
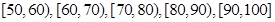 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于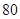 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求 的分布列与均值.
的分布列与均值.
在 中,
中, 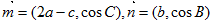 且
且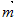 ∥
∥
(1)求角 的大小;
的大小;
(2)若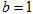 ,当
,当 面积取最大时,求
面积取最大时,求 内切圆的半径.
内切圆的半径.
已知函数 (
(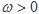 ).
).
(1)求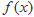 的最小正周期;
的最小正周期;
(2)求函数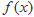 在区间
在区间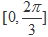 上的取值范围.
上的取值范围.
【选修4-5:不等式选讲】
设函数 (
(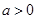 ).
).
(1)证明: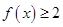 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
【选修4-4:坐标系与参数方程】
已知圆的参数方程为 (
( ,
,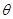 为参数),将圆上所有点的横坐标伸长到原来的
为参数),将圆上所有点的横坐标伸长到原来的 倍,纵坐标不变得到曲线
倍,纵坐标不变得到曲线 ;以坐标原点为极点,以
;以坐标原点为极点,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为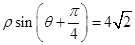 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线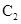 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线 上的动点,求点
上的动点,求点 与曲线
与曲线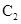 上点的距离的最小值,并求此时
上点的距离的最小值,并求此时 点的坐标.
点的坐标.
【选修4-1:几何证明选讲】
如图,已知圆上的弧 ,过点
,过点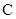 的圆的切线
的圆的切线 与
与 的延长线交于
的延长线交于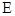 点.
点.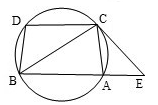
求证:(1) ;
;
(2)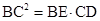 .
.