【选修4-4:坐标系与参数方程】
已知圆的参数方程为 (
( ,
,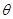 为参数),将圆上所有点的横坐标伸长到原来的
为参数),将圆上所有点的横坐标伸长到原来的 倍,纵坐标不变得到曲线
倍,纵坐标不变得到曲线 ;以坐标原点为极点,以
;以坐标原点为极点,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线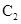 的极坐标方程为
的极坐标方程为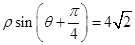 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线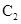 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线 上的动点,求点
上的动点,求点 与曲线
与曲线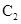 上点的距离的最小值,并求此时
上点的距离的最小值,并求此时 点的坐标.
点的坐标.
(本题满分13分)某厂生产某种产品的年固定成本为250万元,每生产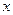 千件,需另投入成本为
千件,需另投入成本为 .当年产量不足80千件时,
.当年产量不足80千件时,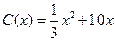 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,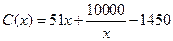 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量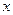 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(本题满分13分) 已知圆C:x2+y2+2x-4y+3=0.
(1)若不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)从圆C外一点P(x,y)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求点P的轨迹方程.
(本题满分13分) 在△ABC中,A,B,C分别是三边a,b,c的对角.设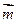 =(cos,sin),
=(cos,sin), =(cos,-sin),
=(cos,-sin),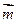 ,
, 的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
(本小题满分12分)已知函数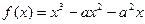 .(Ⅰ)若
.(Ⅰ)若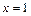 时函数
时函数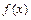 有极值,求
有极值,求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数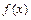 的单调增区间;(Ⅲ)若方程
的单调增区间;(Ⅲ)若方程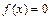 有三个不同的解,分别记为
有三个不同的解,分别记为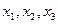 ,证明:
,证明: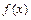 的导函数
的导函数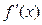 的最小值为
的最小值为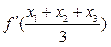 .
.
(本小题满分12分)已知二次函数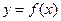 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为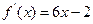 ,数列
,数列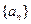 的前n项和为
的前n项和为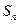 ,点
,点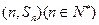 均在函数
均在函数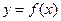 的图像上。(Ⅰ)求数列
的图像上。(Ⅰ)求数列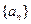 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设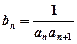 ,
,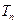 是数列
是数列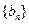 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.