已知抛物线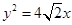 的焦点为椭圆
的焦点为椭圆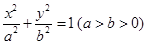 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: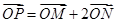 ,直线
,直线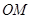 与
与 的斜率之积为
的斜率之积为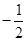 ,证明:存在定点
,证明:存在定点 使
使
得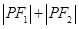 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若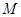 在第一象限,且点
在第一象限,且点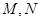 关于原点对称,
关于原点对称,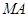 垂直于
垂直于 轴于点
轴于点 ,连接
,连接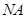 并延长交椭圆于点
并延长交椭圆于点 ,记直线
,记直线 的斜率分别为
的斜率分别为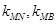 ,证明:
,证明: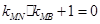 .
.
在1,2,3,…,9这9个自然数中,任取3个数,
(1)记Y表示“任取的3个数中偶数的个数”,求随机变量Y的分布列及其期望;
(2)记X为3个数中两数相邻的组数,例如取出的数为1,2,3,则有这两组相邻的数1,2和2,3,此时X的值为2,求随机变量X的分布列及其数学期望E(X).
某班有6名班干部,其中男生4人,女生2人,任选选3人参加学校的义务劳动。
(1)求男生甲或女生乙被选中的概率
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(B︱A)。
已知函数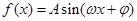 (
( ),该函数所表示的曲线上的一个最高点为
),该函数所表示的曲线上的一个最高点为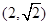 ,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
(1)求 函数解析式;
函数解析式;
(2)求函数 的单调区间;
的单调区间;
(3)若 ,求
,求 的值域。
的值域。
已知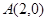 ,
, ,
, ,
, .
.
(1)若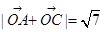 (
(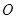 为坐标原点),求
为坐标原点),求 与
与 的夹角;
的夹角;
(2)若 ,求
,求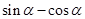 的值.
的值.
已知 ,
,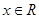 。
。
(1)求 的振幅,最小正周期,对称轴,对称中心。
的振幅,最小正周期,对称轴,对称中心。
(2)说明 是由余弦曲线经过怎样变换得到。
是由余弦曲线经过怎样变换得到。