已知函数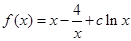 ,其中
,其中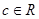 ,
,
(1)当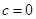 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)讨论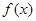 的单调性;
的单调性;
(3)若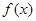 有两个极值点
有两个极值点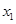 和
和 ,记过点
,记过点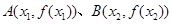 的直线的斜率为
的直线的斜率为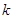 ,问是否存在
,问是否存在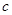 ,使得
,使得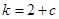 ?若存在,求出
?若存在,求出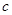 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数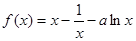
(1)若函数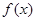 在点
在点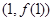 处的切线与圆
处的切线与圆 相切,求
相切,求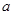 的值;
的值;
(2)当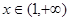 时,函数
时,函数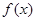 的图像恒在坐标轴
的图像恒在坐标轴 轴的上方,试求出
轴的上方,试求出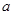 的取值范围.
的取值范围.
已知函数
(1)当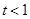 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间。设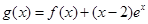 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
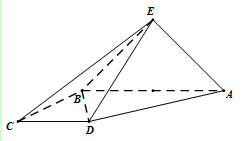
如图,四棱锥 中,面
中,面
 面
面 ,底面
,底面 是直角梯形,侧面
是直角梯形,侧面 是等腰直角三角形.且
是等腰直角三角形.且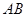 ∥
∥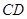 ,
, ,
,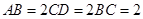 ,
,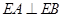 .
.
(1)判断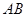 与
与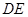 的位置关系;
的位置关系;
(2)求三棱锥 的体积;
的体积;
(3)若点 是线段
是线段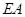 上一点,当
上一点,当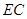 //平面
//平面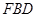 时,求
时,求 的长.
的长.
已知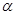 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
.
(Ⅰ)求函数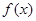 的表达式;
的表达式;
(Ⅱ)求数列 的前
的前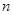 项和
项和 .
.
 的外接圆半径
的外接圆半径 ,角
,角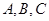 的对边分别是
的对边分别是 ,且
,且 .
.
(1)求角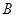 和边长
和边长 ;
;
(2)求 的最大值及取得最大值时的
的最大值及取得最大值时的 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.