已知平面上三个向量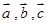 ,其中
,其中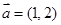 .
.
(1)若 ,且
,且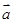 ∥
∥ ,求
,求 的坐标;
的坐标;
(2)若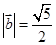 ,且
,且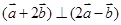 ,求
,求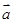 与
与 夹角
夹角 .
.
(本小题满分12分)
已知点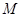 是椭圆
是椭圆 :
: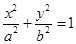
 上一点,
上一点, 分别为
分别为 的左右焦点,
的左右焦点, ,
, ,
, 的面积为
的面积为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过椭圆右焦点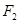 的直线
的直线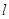 和椭圆交于两点
和椭圆交于两点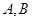 ,是否存在直线
,是否存在直线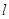 ,使得△
,使得△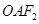 与△
与△ 的面积比值为
的面积比值为 ?若存在,求出直线
?若存在,求出直线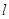 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分)
如图,平面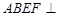 平面
平面 ,四边形
,四边形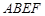 为矩形,
为矩形,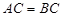 .
. 为
为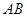 的中点,
的中点, .
.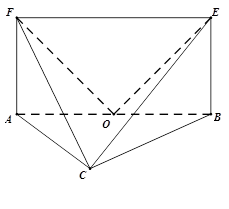

(Ⅰ)求证: ;
;
(Ⅱ)若二面角 的余弦值为
的余弦值为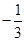 时,求
时,求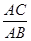 的值.
的值.
(本小题满分12分)
某家电生产企业市场营销部对本厂生产的某种电器进行了市场调查,发现每台的销售利润与该电器的无故障使用时间 (单位:年)有关.若
(单位:年)有关.若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元,设每台该种电器的无故障使用时间
元,设每台该种电器的无故障使用时间 ,
, ,
, 这三种情况发生的概率分别是
这三种情况发生的概率分别是 ,又知
,又知 是方程
是方程 的两个根,且
的两个根,且 .
.
(1)求 的值;
的值;
(2)记 表示销售两台该种电器的销售利润总和,求
表示销售两台该种电器的销售利润总和,求 的分布列及期望.
的分布列及期望.
(本小题满分12分)
已知向量 ,
,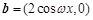
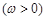 ,函数
,函数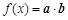 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为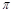 .
.
(Ⅰ)求函数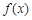 在
在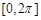 上的单调递增区间;
上的单调递增区间;
(Ⅱ)将函数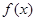 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数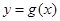 的图象.若
的图象.若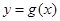 在
在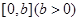 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
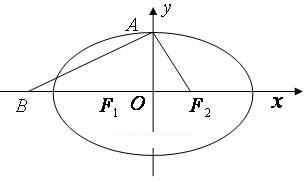
设椭圆 的左、右焦点分别为
的左、右焦点分别为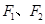 ,上顶点为
,上顶点为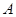 ,在
,在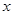 轴负半轴上有一点
轴负半轴上有一点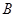 ,满足
,满足 ,且
,且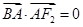 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过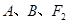 三点的圆与直线
三点的圆与直线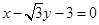 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点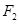 作斜率为
作斜率为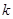 的直线
的直线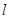 与椭圆
与椭圆 交于
交于 两点,线段
两点,线段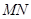 的中垂线与
的中垂线与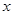 轴相交于
轴相交于 ,求实数
,求实数 的取值范围.
的取值范围.