已知各项均为正数的数列
满足
, 且
,其中
.
(1) 求数列的通项公式；
(2) 设数列
满足
,是否存在正整数
，使得
成等比数列？若存在，求出所有的
的值；若不存在，请说明理由。
(3) 令
,记数列
的前
项和为
,其中,证明：
。
（本小题满分12分）.
已知函数
在
上是减函数，在
上是增函数，函数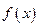
在
上有三个零点，且1是其中一个零点．
（1）求
的值； （2）求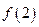
的取值范围；
（本小题满分12分）如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行
四边形，且DC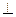
平面ABC．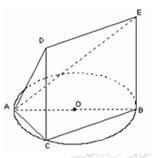
（1）证明：平面ACD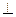平面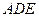
；
（2）若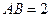
，
，
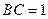，试求该简单组合体的体积V．
（本小题满分12分）
某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：每一组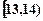
；第二组
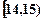……第五组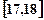
．下图是按上述分组方法得到的频率分布直方图.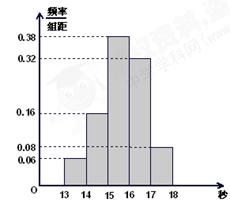 
（I）若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
（II）设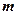
、
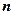表示该班某两位同学的百米测试成绩，且已知
.
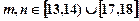求事件“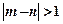
”的概率.
（本小题满分12分）
已知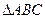
的三个内角A、B、C所对的边分别为
,向量
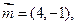
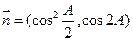，且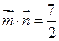
．
（1）求角A的大小；（2）若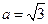
，试判断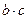
取得最大值时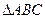形状．
如图，已知椭圆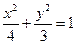
上两定点
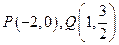,直线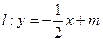
与椭圆相交于A,B两点（异于P,Q两点）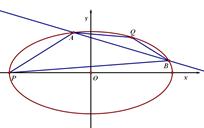
（1）求证：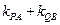
为定值；
（2）当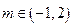
时，求A、P、B、Q四点围成的四边形面积的最大值。