在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE= a,BC=DE=a,
a,BC=DE=a,
∠EAB=∠ABC=∠DEA=90°.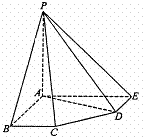 (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE;
(2)若G为PE中点,求证: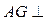 平面PDE
平面PDE
(3)求二面角A-PD-E的正弦值;
(4)求点C到平面PDE的距离
(本小题满分12分)在锐角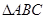 中,角
中,角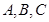 所对边分别为
所对边分别为 ,已知
,已知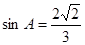 .
.
(Ⅰ)求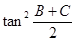 的值;
的值;
(Ⅱ)若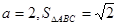 ,求
,求 的值.
的值.
(I) 已知抛物线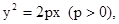 过焦点
过焦点 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;
(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点 的动直线 l 交抛物线于
的动直线 l 交抛物线于 两点, 存在定点
两点, 存在定点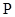 ,使得
,使得 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.
设数列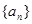 的首项
的首项 ,前
,前 项和
项和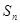 满足关系式:
满足关系式: 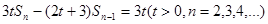
(1)求证:数列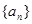 是等比数列;
是等比数列;
(2)设数列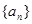 是公比为
是公比为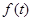 ,作数列
,作数列 ,使
,使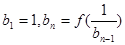
 ,
,
求和: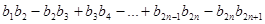 ;
;
(3)若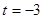 ,设
,设 ,
, ,
,
求使
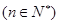 恒成立的实数k的范围.
恒成立的实数k的范围.
如图,四边形 中(图1),
中(图1),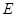 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为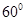 (如图2)
(如图2)
(1)求证: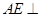 平面
平面 ;
;
(2)求二面角A—DC—B的余弦值。
已知函数f(x)=ln x-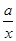 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为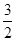 ,求a的值;
,求a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.