一个几何体是由圆柱 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中 ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
分别指出由下列各组命题构成的逻辑关联词“或”、“且”的真假.
(1)p: 梯形有一组对边平行;q:梯形有一组对边相等.
(2)p: 1是方程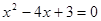 的解;q:3是方程
的解;q:3是方程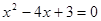 的解.
的解.
(3)p: 不等式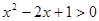 解集为R;q: 不等式
解集为R;q: 不等式 解集为Æ.
解集为Æ.
(4)p: 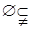
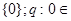 Æ
Æ
已知 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合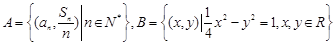 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2) 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有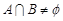 .
.
写出下列命题的逆命题、否命题、逆否命题,并指出他们的真假:
(1)若xy=0,则x,y中至少有一个是0;
(2)若x>0,y>0,则xy>0;
把命题“未位数是0的整数可以被5整除”改写为“若p则q”的形式,并写出它的逆命题、否命题与逆否命题
等比数列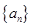 中,
中,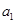 ,
, ,
,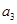 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且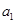 ,
, ,
,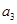 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ)求数列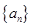 的通项公式;
的通项公式;
(Ⅱ)若数列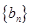 满足:
满足: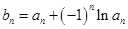 ,求数列
,求数列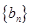 的前
的前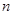 项和
项和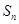 .
.