已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
已知数列 满足
满足 ,求数列
,求数列 的通项公式。
的通项公式。
已知数列 满足
满足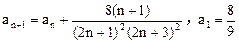 ,求数列
,求数列 的通项公式。
的通项公式。
(本小题满分14分)a 为常数,求函数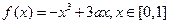 的最大值。
的最大值。
(本小题满分12分)在△ABC中,∠C = 90o ,BC = 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF =" y" ,(1)求y与x的函数关系式;(2)正方形EFGH的面积是否有最大值?试证明你的结论。
(本小题满分12分)某农场在相同条件下种植甲、乙两种水稻各100 亩,它们的收获情况如下:
甲乙
| 亩产量(单位:千克) |
300 |
320 |
330 |
340 |
| 亩数 |
20 |
25 |
40 |
15 |
| 亩产量(单位:千克) |
310 |
320 |
330 |
340 |
| 亩数 |
30 |
20 |
40 |
10 |
试说明哪种水稻的产量比较稳定?