已知数列{an}的前n项和Sn=n2+1,数列{bn}是首项为1,公比为b的等比数列.
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Tn.
(12分)函数f(x)定义在R上的偶函数,当x≥0时,f(x)=
(1)写出f(x)单调区间;
(2)函数的值域;
已知集合U={x|-3≤x≤3},M={x|-1<x<1},CUN={x|0<x<2},求 集合N, M∩(CUN),M∪N.
(本题满分12分) 已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为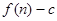 ,数列
,数列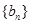
 的首项为
的首项为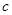 ,且前
,且前 项和
项和 满足
满足 -
- =
= +
+ (
( ).
).
(1)求数列 和
和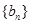 的通项公式;
的通项公式;
(2)若数列{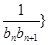 前
前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少?
是多少?
(本题满分12分)已知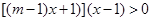 ,其中0<
,其中0< 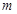 <2,
<2,
(1)解不等式。
(2)若x>1时,不等式恒成立,求实数m的范围。
(本题满分12分)在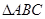 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为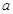 、
、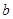 、
、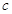 ,
,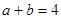 ,C
,C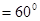
(1)若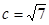 ,求边
,求边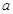 ,
,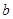 ;
;
(2)求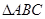 的面积的最大值.
的面积的最大值.