已知集合U={x|-3≤x≤3},M={x|-1<x<1},CUN={x|0<x<2},求 集合N, M∩(CUN),M∪N.
已知全集 ,
, ,
, ,
,
(Ⅰ)求 ;
;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
设函数 .
.
(1)当 时,记函数
时,记函数 在[0,4]上的最大值为
在[0,4]上的最大值为 ,求
,求 的最小值;
的最小值;
(2)存在实数 ,使得当
,使得当 时,
时, 恒成立,求
恒成立,求 的最大值及此时
的最大值及此时 的值.
的值.
已知抛物线 :
: ,过焦点F的直线
,过焦点F的直线 与抛物线交于
与抛物线交于 两点(
两点( 在第一象限).
在第一象限).
(1)当 时,求直线
时,求直线 的方程;
的方程;
(2)过点 作抛物线
作抛物线 的切线
的切线 与圆
与圆 交于不同的两点
交于不同的两点 ,设
,设 到
到 的距离为
的距离为 ,求
,求
 的取值范围.
的取值范围.
在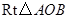 中,
中,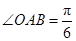 ,斜边
,斜边 .
.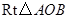 以直线
以直线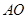 为轴旋转得到
为轴旋转得到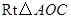 ,且二面角
,且二面角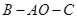 是直二面角,动点
是直二面角,动点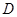 在斜边
在斜边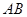 上。
上。
(1)求证:平面 平面
平面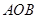 ;
;
(2)当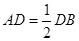 时,求异面直线
时,求异面直线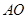 与
与 所成角的正切值;
所成角的正切值;
(3)求 与平面
与平面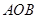 所成最大角的正切值.
所成最大角的正切值.
设各项均为正数的数列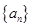 的前
的前 项和为
项和为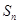 ,满足
,满足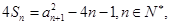 且
且 .
.
(1) 求数列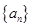 的通项公式;
的通项公式;
(2) 证明:对一切正整数 ,有
,有 .
.