有一副直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4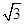
，将这副直角三角板按如图(1)所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．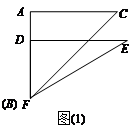
(1)如图(2)，当三角板DEF运动到点D与点A重合时，设EF与BC交于点M，则∠EMC= 度；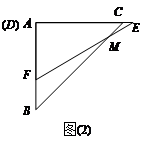
(2)如图(3)，在三角板DEF运动过程中，当EF经过点C时，求FC的长；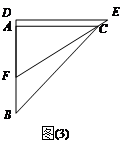
(3)在三角板DEF运动过程中，当D在BA的延长线上时，设BF=x，两块三角板重迭部分的面积为y．求y与x的函数关系式，并求出对应的x取值范围．
因式分解：
（1）x3－4x；（2）（x－1）（x－4）－10．
如图，EF∥AD，∠1=∠2，∠BAC=80°，将求∠AGD的过程填写完整．
∵EF//AD，
∴∠2=（）
又∵∠1=∠2，
∴∠1=∠3（）
∴AB//（）
∴∠BAC＋=180°（）
∵∠BAC=80°，
∴∠AGD=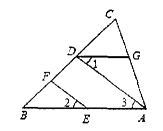
解方程组（1）
（2）
计算：
（1）
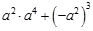；（2）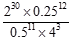
．
如图1，已知正方形ABCD，把一个直角与正方形叠合，使直角顶点与一重合，当直角的一边与BC相交于E点，另一边与CD的延长线相交于F点时．
（1）证明：BE=DF；
（2）如图2，作∠EAF的平分线交CD于G点，连接EG．证明：BE＋DG=EG；
（3）如图3，将图1中的“直角”改为“∠EAF=45°”，当∠EAF的一边与BC的延长线相交于E点，另一边与CD的延长线相交于F点，连接EF．线段BE，DF和EF之间有怎样的数量关系？并加以证明．