(本小题共13分)如图,矩形ABCD中,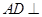 平面ABE
平面ABE ,BE=BC,F为CE上的点,且
,BE=BC,F为CE上的点,且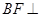 平面ACE。
平面ACE。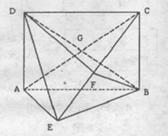
(1)求证: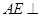 平面BCE;
平面BCE;
(2)求证:AE//平面BFD。
(本小题共13分)已知
(1)求 的值;
的值;
(2)求函数 的值域。
的值域。
已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点。
(1)若以AB线段为直径的圆过坐标原点,求实数a的值。
(2)是否存在这样的实数a,使A、B两点关于直线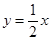 对称?说明理由。
对称?说明理由。
已知椭圆的中心在原点,离心率为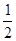 ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数).
(Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线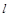 与y轴交于点M.若
与y轴交于点M.若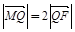 ,求直线
,求直线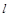 的斜率.
的斜率.
命题 实数
实数 满足
满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足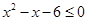 或
或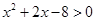 ,且
,且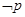 是
是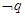 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.