已知圆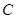 的方程为:
的方程为: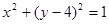 ,直线的方程为
,直线的方程为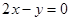 ,点
,点 在直线上,过点
在直线上,过点 作圆
作圆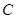 的切线
的切线 ,切点为
,切点为 .
.
(1)若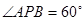 ,求点
,求点 的坐标;
的坐标;
(2)若点 的坐标为
的坐标为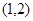 ,过点
,过点 的直线与圆
的直线与圆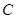 交于
交于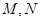 两点,当
两点,当 时,求直线
时,求直线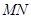 的方程;
的方程;
(3)求证:经过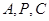 (其中点
(其中点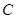 为圆
为圆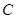 的圆心)三点的圆必经过定点,并求出所有定点的坐标.
的圆心)三点的圆必经过定点,并求出所有定点的坐标.
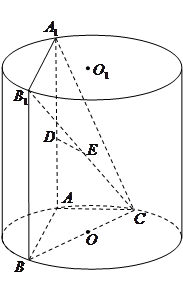
如图,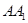 、
、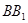 为圆柱
为圆柱 的母线,
的母线,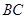 是底面圆
是底面圆 的直径,
的直径,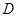 、
、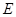 分别是
分别是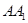 、
、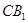 的中点,
的中点, .
.
(1)证明: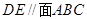 ;
;
(2)证明: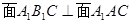 ;
;
(3)求四棱锥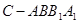 与圆柱
与圆柱 的体积比.
的体积比.
从某学校高三年级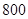 名学生中随机抽取
名学生中随机抽取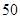 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于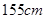 和
和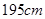 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组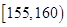 .第二组
.第二组 ; 第八组
; 第八组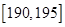 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
| 组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 样本数 |
(2)估计这所学校高三年级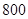 名学生中身高在
名学生中身高在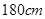 以上(含
以上(含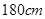 )的人数;
)的人数;
(3)在样本中,若第二组有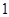 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有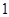 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
向量 ,
, ,已知
,已知 ,且有函数
,且有函数 .
.
(1)求函数 的周期;
的周期;
(2)已知锐角 的三个内角分别为
的三个内角分别为 ,若有
,若有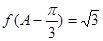 ,边
,边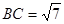 ,
,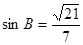 ,求
,求 的长及
的长及 的面积.
的面积.
设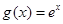 ,
, ,其中
,其中 是常数,且
是常数,且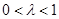 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数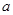 ,存在正数
,存在正数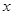 ,使不等式
,使不等式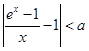 成立;
成立;
(3)设 ,且
,且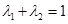 ,证明:对任意正数
,证明:对任意正数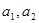 都有:
都有: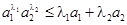 .
.
知数列 的首项
的首项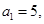 前
前 项和为
项和为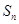 ,且
,且
(1)证明:数列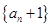 是等比数列;
是等比数列;
(2)令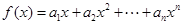 ,求函数
,求函数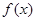 在点
在点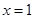 处的导数
处的导数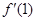 ,并比较
,并比较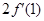 与
与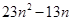 的大小.
的大小.