某商品每件成本5元，售价14元，每星期卖出75件.如果降低价格，销售量可以增加，且每星期多卖出的商品件数
与商品单价的降低值
（单位：元，
）的平方成正比，已知商品单价降低1元时，一星期多卖出5件.
（1）将一星期的商品销售利润
表示成的函数；
（2）如何定价才能使一个星期的商品销售利润最大？
（本小题满分16分）
数列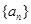
的前n项和为
，存在常数A，B，C，使得
对任意正整数n都成立。
（１）若数列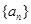为等差数列，求证：3A－B＋C＝０；
（２）若
设
数列
的前ｎ项和为
，求；
（３）若C=0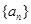，是首项为1的等差数列，设
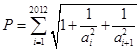，求不超过P的最大整数的值。
（本小题满分16分）
已知函数
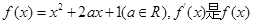的导函数。
（1）若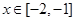
，不等式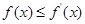
恒成立，求a的取值范围；
（2）解关于x的方程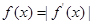
；
（3）设函数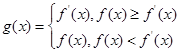
，求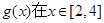
时的最小值；
（本小题满分16分）
如图，在平面直角坐标系xoy中，圆C：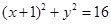
，点F（1，0），E是圆C上的一个动点，EF的垂直平分线PQ与CE交于点B，与EF交于点D。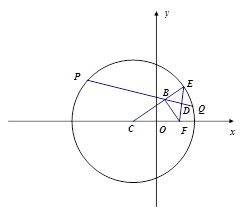
（１）求点B的轨迹方程；
（２）当D位于ｙ轴的正半轴上时，求直线PQ的方程；
（３）若G是圆上的另一个动点，且满足FG⊥FE。记线段EG的中点为M，试判断线段OM的长度是否为定值？若是，求出该定值;若不是，说明理由。
（本小题满分14分）
在一个半径为1的半球材料中截取三个高度均为h的圆柱，其轴截面如图所示，设三个圆柱体积之和为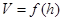
。
（１）求f(h)的表达式，并写出h的取值范围是 ；
（２）求三个圆柱体积之和V的最大值；
（本小题满分14分）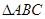
中，角A，B,C的对边分别是
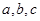且满足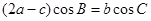
（１）求角B的大小；
（２）若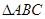的面积为为
，求
的值；