定义:若数列{An}满足An+1=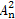 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
(1)证明:数列{2an+1}是 “平方递推数列”,且数列{lg(2an+1)}为等比数列.
(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项公式及Tn关于n的表达式.
(12分)已知数列{ }的前n项和为
}的前n项和为 ,
, ,满足
,满足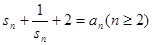 ,计算
,计算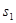 ,
,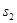 ,
, ,
,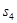 ,并猜想
,并猜想 的表达式.
的表达式.
(10分) 解不等式|x-2|+|x-3|<9
(10分)设复数z=m+1+(m-1)i,试求m取何值时
(1)Z是实数;
(2)Z是虚数;
(3)Z对应的点位于复平面的第一象限
选修4—5;不等式选讲
已知a和b是任意非零实数.
(1)求 的最小值.
的最小值.
(2)若不等式 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
选修4—4;坐标系与参数方程
在平面直角坐标系xOy中,已知曲线 ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.
(1)将曲线 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、2倍后得到曲线
、2倍后得到曲线
试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;
(2)在曲线 上求一点P,使点P到直线
上求一点P,使点P到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.