在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,q= .
.
(1)求an与bn.
(2)证明: ≤
≤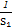 +
+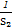 +…+
+…+ <
< .
.
在直角坐标系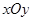 中,点P到两点
中,点P到两点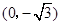 ,
,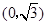 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为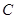 ,直线
,直线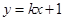 与C交于A,B两点.(Ⅰ)写出C的方程;(Ⅱ)若
与C交于A,B两点.(Ⅰ)写出C的方程;(Ⅱ)若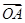
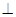
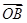 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|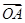 |>|
|>|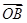 |.
|.
、已知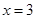 是函数
是函数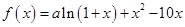 的一个极值点.
的一个极值点.
(Ⅰ)求 ;(Ⅱ)求函数
;(Ⅱ)求函数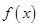 的单调区间;
的单调区间;
(Ⅲ)若直线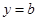 与函数
与函数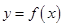 的图象有3个交点,求
的图象有3个交点,求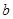 的取值范围.
的取值范围.
已知函数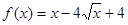 (x≥4)的反函数为
(x≥4)的反函数为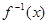 ,数列
,数列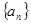 满足:a1=1,
满足:a1=1,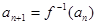 ,(
,(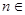 N*),数列
N*),数列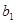 ,
,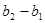 ,
,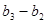 ,…,
,…,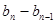 是首项为1,公比为
是首项为1,公比为 的等比数列.
的等比数列.
(Ⅰ)求证:数列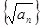 为等差数列;(Ⅱ)若
为等差数列;(Ⅱ)若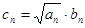 ,求数列
,求数列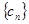 的前n项和
的前n项和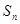 .
.
已知函数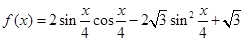 .
.
(Ⅰ)求函数 的最小正周期及最值;(Ⅱ)令
的最小正周期及最值;(Ⅱ)令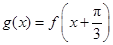 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
已知数列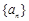 的前n项和
的前n项和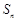 满足:
满足: (a为常数,且
(a为常数,且 ).
).
(Ⅰ)求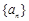 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设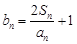 ,若数列
,若数列 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设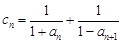 ,数列
,数列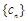 的前n项和为Tn .
的前n项和为Tn .
求证: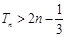 .
.