已知△ABC的内角为A、B、C,其对边分别为a、b、c,B为锐角,向量m=(2sin B,- ),n=
),n= ,且m∥n
,且m∥n
(1)求角B的大小;
(2)如果b=2,求S△ABC的最大值.
已知直线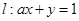 在矩阵
在矩阵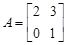 对应的变换作用下变为直线
对应的变换作用下变为直线 .
.
(1)求实数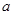 ,
,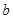 的值;
的值;
(2)若点 在直线
在直线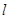 上,且
上,且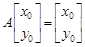 ,求点
,求点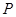 的坐标.
的坐标.
若数列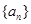 满足
满足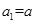 且
且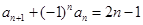 (其中
(其中 为常数),
为常数),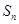 是数列
是数列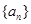 的前
的前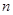 项和,数列
项和,数列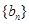 满足
满足 .
.
(1)求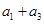 的值;
的值;
(2)试判断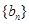 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求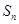 (用
(用 表示).
表示).
已知函数 ,
, 为常数.
为常数.
(1)若函数 在
在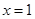 处的切线与
处的切线与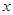 轴平行,求
轴平行,求 的值;
的值;
(2)当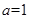 时,试比较
时,试比较 与
与 的大小;
的大小;
(3)若函数 有两个零点
有两个零点 、
、 ,试证明
,试证明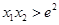 .
.
已知椭圆 的右准线
的右准线 ,离心率
,离心率 ,
,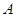 ,
,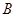 是椭圆上的两动点,动点
是椭圆上的两动点,动点 满足
满足 ,(其中
,(其中 为常数).
为常数).
(1)求椭圆标准方程;
(2)当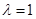 且直线
且直线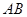 与
与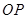 斜率均存在时,求
斜率均存在时,求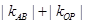 的最小值;
的最小值;
(3)若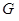 是线段
是线段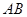 的中点,且
的中点,且 ,问是否存在常数
,问是否存在常数 和平面内两定点
和平面内两定点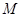 ,
,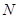 ,使得动点
,使得动点 满足
满足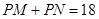 ,若存在,求出
,若存在,求出 的值和定点
的值和定点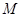 ,
,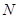 ;若不存在,请说明理由.
;若不存在,请说明理由.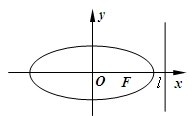
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔 、
、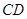 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知 ,
,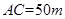 ,当
,当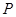 为
为 中点时,
中点时,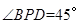 .
.
(1)求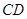 的长;
的长;
(2)试问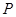 在线段
在线段 的何处时,
的何处时,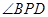 达到最大.
达到最大.
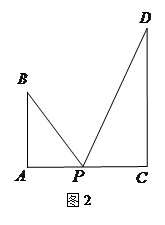
|