已知函数f(x)=2sin (0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(1)求点A、B的坐标以及 ·
·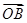 的值;
的值;
(2)设点A、B分别在角α、β的终边上,求tan(α-2β)的值.
(1)已知方程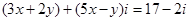 ,求实数
,求实数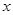 与
与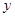 的值;
的值;
(2)已知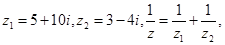 求
求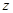 .
.
设等差数列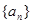 的公差
的公差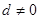 ,等比数列
,等比数列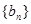 公比为
公比为 ,且
,且 ,
,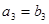 ,
,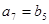
(1)求等比数列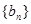 的公比
的公比 的值;
的值;
(2)将数列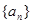 ,
,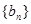 中的公共项按由小到大的顺序排列组成一个新的数列
中的公共项按由小到大的顺序排列组成一个新的数列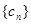 ,是否存在正整数
,是否存在正整数 (其中
(其中 )使得
)使得 和
和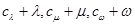 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数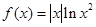 .
.
(1)判断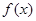 奇偶性, 并求出函数
奇偶性, 并求出函数 的单调区间;
的单调区间;
(2)若函数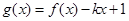 有零点,求实数
有零点,求实数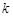 的取值范围.
的取值范围.
椭圆 的离心率为
的离心率为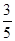 ,两焦点分别为
,两焦点分别为 ,点M是椭圆C上一点,
,点M是椭圆C上一点, 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆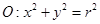 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为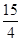 .
.
(1)求椭圆C以及圆O的方程;
(2)当点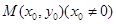 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线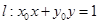 与圆O的位置关系.
与圆O的位置关系.
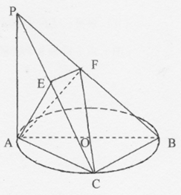
如图,已知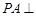 ⊙
⊙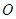 所在的平面,
所在的平面,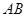 是⊙
是⊙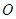 的直径,
的直径,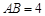 ,C是⊙
,C是⊙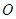 上一点,且
上一点,且
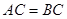 ,
,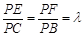 .
.
(1) 求证: ;
;
(2) 求证: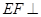
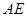 ;
;
(3)当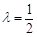 时,求三棱锥
时,求三棱锥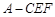 的体积.
的体积.