设正项数列{an}的前n项和是Sn,若{an}和{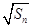 }都是等差数列,且公差相等.
}都是等差数列,且公差相等.
(1)求{an}的通项公式;
(2)若a1,a2,a5恰为等比数列{bn}的前三项,记数列cn=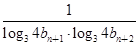 ,数列{cn}的前n项和为Tn,求Tn.
,数列{cn}的前n项和为Tn,求Tn.
(本小题满分12分)
已知数列{an}的前n项和为Sn,点 在直线
在直线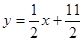 上.数列{bn}满足
上.数列{bn}满足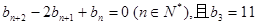 ,前9项和为153.
,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设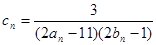 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式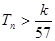 对一切
对一切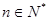 都成立的最大正整数k的值.
都成立的最大正整数k的值.
(本小题满分12分)
在 中,角
中,角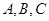 所对的三边分别为
所对的三边分别为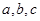 成等比数列,且
成等比数列,且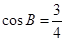 .
.
(1)求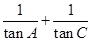 的值;
的值;
(2)设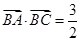 ,求
,求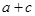 的值.
的值.
(本小题满分12分)在数列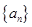 中,
中, 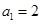 ,
,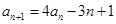 ,
,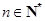 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(II)求数列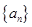 的前
的前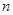 项和
项和 .
.
(Ⅲ)证明对任意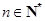 ,不等式
,不等式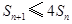 成立.
成立.
(本小题满分12分)设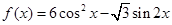 .
.
(Ⅰ)求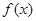 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角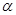 满足
满足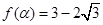 ,求
,求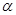 的值.
的值.
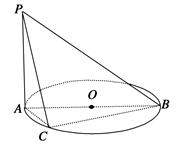
(本题满分12分)如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.