在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC的中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且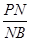 =
= .
.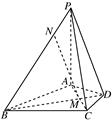
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)设平面PAB∩平面PCD=l,试问直线l是否与直线CD平行,请说明理由.
如图,在正方体 中,
中, 、
、 、
、 分别是
分别是 ,
, ,
, 的中点.
的中点.
(1) 平面
平面
(2) 平面
平面 .
.
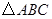 中内角
中内角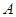 ,
,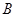 ,
,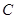 的对边分别为
的对边分别为 ,
,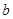 ,
,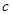 ,向量
,向量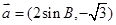 ,
,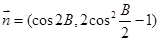 ,且
,且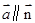 .
.
(1)求锐角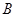 的大小;
的大小;
(2)如果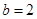 ,求
,求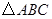 的面积
的面积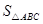 的最大值.
的最大值.
已知椭圆C的方程是
 ,点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为
,点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为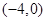 ,且过点
,且过点 .
.
(1)求椭圆C的方程;
(2)已知F是椭圆C的右焦点,以AF为直径的圆记为圆M,试问:过P点能否引圆M的切线,若能,求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积;若不能,说明理由.
(本小题满分12分)如图,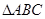 内接于圆O,AB是圆O的直径,
内接于圆O,AB是圆O的直径, ,
,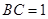 ,
,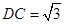 ,四边形DCBE为平行四边形,
,四边形DCBE为平行四边形,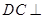 平面ABC.
平面ABC.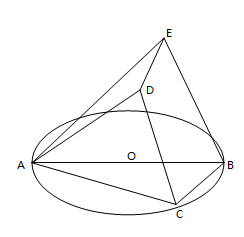
(1)证明:平面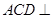 平面ADE;
平面ADE;
(2)在CD上是否存在一点M,使得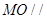 平面ADE?证明你的结论.
平面ADE?证明你的结论.
已知抛物线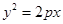
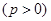 焦点为F,抛物线上横坐标为
焦点为F,抛物线上横坐标为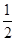 的点到抛物线顶点的距离与其到准线的距离相等.
的点到抛物线顶点的距离与其到准线的距离相等.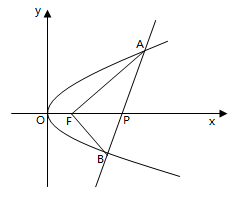
(1)求抛物线的方程;
(2)设过点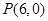 的直线
的直线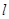 与抛物线交于A,B两点,若以AB为直径的圆过点F,求直线
与抛物线交于A,B两点,若以AB为直径的圆过点F,求直线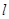 的方程.
的方程.