在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos  =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为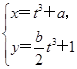 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
如图,四棱锥 的底面
的底面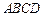 为一直角梯形,其中
为一直角梯形,其中 ,
,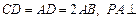 底面
底面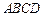 ,
,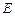 是
是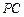 的中点.
的中点.
(1)试用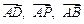 表示
表示 ,并判断直线
,并判断直线 与平面
与平面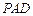 的位置关系;
的位置关系;
(2)若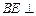 平面
平面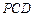 ,求异面直线
,求异面直线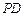 与
与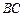 所成角的余弦值.
所成角的余弦值.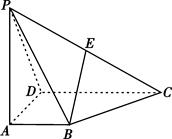
第四届中国国际航空航天博览会于2010年11月在珠海举行,一次飞行表演中,一架直升飞机在海拔800m的高度飞行,从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示).
(1)试计算这个海岛的宽度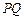 .
.
(2)若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为45°和30°,他们估计P、Q两处距离大约为600m,由此试估算出观测者甲(在P处)到飞机的直线距离. 
等比数列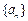 的公比为q,第8项是第2项与第5项的等差中项.
的公比为q,第8项是第2项与第5项的等差中项.
(1)求公比q;
(2)若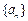 的前n项和为
的前n项和为 ,判断
,判断 是否成等差数列,并说明理由.
是否成等差数列,并说明理由.
过直角坐标平面 中的抛物线
中的抛物线 的焦点
的焦点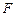 作一条倾斜角为
作一条倾斜角为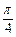 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.
(1)求直线AB的方程;
(2)试用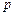 表示A、B之间的距离;
表示A、B之间的距离;
(3)当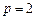 时,求
时,求 的余弦值.
的余弦值.
参考公式: .
.
第四届中国国际航空航天博览会于2010年11月在珠海举行,一次飞行表演中,一架直升飞机在海拔800m的高度飞行,从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示).
(1)试计算这个海岛的宽度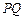 .
.
(2)若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为45°和30°,他们估计P、Q两处距离大约为600m,由此试估算出观测者甲(在P处)到飞机的直线距离.