甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为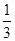 ,且各局胜负相互独立,比赛停止时一共已打
,且各局胜负相互独立,比赛停止时一共已打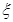 局:
局:
(1)列出随机变量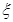 的分布列;
的分布列;
(2)求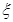 的期望值E
的期望值E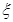 .
.
(本小题满分12分)已知 ,设
,设 的最小正周期为
的最小正周期为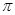 .
.
(Ⅰ)求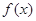 的单调增区间;
的单调增区间;
(Ⅱ)当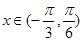 时,求
时,求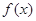 的值域;
的值域;
(Ⅲ)求满足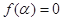 且
且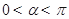 的角
的角 的值.
的值.
(本小题满分12分)有一种新型的洗衣液,去污速度特别快.已知每投放 且
且 个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度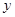 (克/升)随着时间
(克/升)随着时间 (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为 ,其中
,其中 .根据经验,当水中洗衣液的浓度不低于
.根据经验,当水中洗衣液的浓度不低于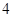 (克/升)时,它才能起到有效去污的作用.
(克/升)时,它才能起到有效去污的作用.
(Ⅰ)若投放 个单位的洗衣液,
个单位的洗衣液, 分钟时水中洗衣液的浓度为
分钟时水中洗衣液的浓度为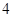 (克/升),求
(克/升),求 的值 ;
的值 ;
(Ⅱ)若投放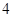 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
(本小题满分12分)在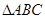 中,内角
中,内角 所对的边分别为
所对的边分别为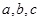 ,已知
,已知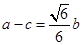 ,
, .
.
(Ⅰ)求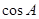 的值;
的值;
(Ⅱ)求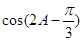 的值.
的值.
已知关于 的不等式:
的不等式: 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(1) 求整数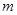 的值;
的值;
(2 )已知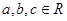 ,若
,若 ,求
,求 的最大值
的最大值
已知曲线 的参数方程为
的参数方程为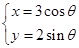 (
(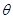 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换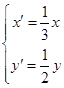 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程;
的普通方程;
(2)若点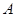 在曲线
在曲线 上,点
上,点
 ,当点
,当点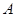 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点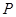 的轨迹方程.
的轨迹方程.