如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2, ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为α,β,且α+β=π,试问直线l是否过定点?若过,求该定点的坐标.
如图,四棱锥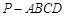 的底面是直角梯形,
的底面是直角梯形,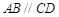 ,
,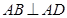 ,
,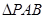 和
和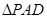 是两个边长为
是两个边长为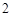 的正三角形,
的正三角形,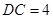 ,
, 为
为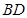 的中点,
的中点,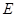 为
为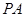 的中点.
的中点.
(Ⅰ)求证: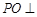 平面
平面 ;
;
(Ⅱ)求证: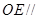 平面
平面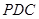 ;
;
(Ⅲ)求直线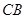 与平面
与平面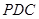 所成角的正弦值.
所成角的正弦值.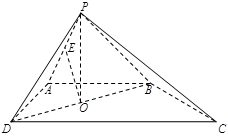
已知椭圆 的焦点分别为
的焦点分别为 、
、 ,长轴长为6,设直线
,长轴长为6,设直线 交椭圆
交椭圆 于A、B两点。(Ⅰ)求线段AB的中点坐标;(Ⅱ)求
于A、B两点。(Ⅰ)求线段AB的中点坐标;(Ⅱ)求 的面积。
的面积。
已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,
求:(Ⅰ)动点M的轨迹方程;
(Ⅱ)若N为线段AM的中点,试求点N的轨迹.
设集合A= ,关于x的不等式
,关于x的不等式 的解集为B(其中a<0),设
的解集为B(其中a<0),设 ,
,  ,且
,且 是
是 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.