如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=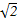 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.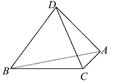
(1)当平面ADB⊥平面ABC时,求CD.
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
(本题12分)
如图,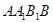 是圆柱的轴截面,
是圆柱的轴截面,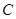 是底面圆周上异于
是底面圆周上异于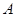 ,
,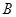 的一点,
的一点,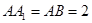 .
.
(1)求证:平面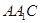 ⊥平面
⊥平面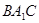 .
.
(2)求几何体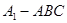 的体积
的体积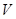 的最大值.
的最大值.
(本题10分)
按规定:车辆驾驶员血液酒精浓度在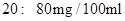 (不含
(不含 )之间,属酒后驾车;在
)之间,属酒后驾车;在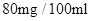 (含
(含 )以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了
)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了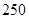 辆机动车,查出酒后驾车和醉酒驾车的驾驶员
辆机动车,查出酒后驾车和醉酒驾车的驾驶员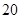 人,右图是对这
人,右图是对这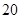 人血液中酒精含量进行检查所得结果的频率分布直方图.
人血液中酒精含量进行检查所得结果的频率分布直方图.
(1)根据频率分布直方图,求:此次抽查的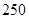 人中,醉酒驾车的人数;
人中,醉酒驾车的人数;
(2)从血液酒精浓度在 范围内的驾驶员中任取
范围内的驾驶员中任取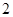 人,求恰有
人,求恰有 人属于醉酒驾车的概率.
人属于醉酒驾车的概率.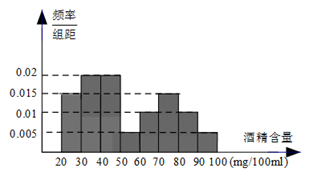
已知函数
(1)若a=1,求函数f(x)的零点;
(2)若函数f(x)在[-1,+∞)上为增函数,求a的取值范围.
某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记资金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;
(2)如果业务员老张获得5.5万元的资金,那么他的销售利润是多少万元?
已知函数f(x)=x2+2ax+2,x∈[-5,5].
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数