已知椭圆的中心为坐标原点,短轴长为2,一条准线的方程为l:x=2.
(1)求椭圆的标准方程.
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
如图,三棱柱
中,侧面
为菱形,
.
(Ⅰ)证明:
;
(Ⅱ)若
,
,
,求二面角
的余弦值.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图: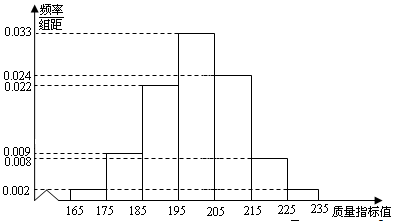
(I)求这500件产品质量指标值的样本平均值
和样本方差
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标
服从正态分布 ,其中
近似为样本平均数
,
,其中
近似为样本平均数
, 近似为样本方差
.
近似为样本方差
.
(i)利用该正态分布,求
;
(ii)某用户从该企业购买了100件这种产品,记
表示这100件产品中质量指标值位于区间
的产品件数.利用(i)的结果,求
.
附:
若 则
则 ,
, 。
。
已知数列
的前
项和为
,
,
,
,其中
为常数,
(I)证明:
;
(II)是否存在
,使得
为等差数列?并说明理由.
已知函数
,其中
,
为自然对数的底数.
(Ⅰ)设
是函数
的导函数,求函数
在区间
上的最小值;
(Ⅱ)若
,函数
在区间
内有零点,求
的取值范围
已知椭圆
的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆
的标准方程;
(2)设
为椭圆
的左焦点,
为直线
上任意一点,过
作
的垂线交椭圆
于点
.
(i)证明:
平分线段
(其中
为坐标原点);
(ii)当
最小时,求点
的坐标.