已知圆C与两圆x2+(y+4)2=1,x2+(y-2)2=1外切,圆C的圆心轨迹方程为L,设L上的点与点M(x,y)的距离的最小值为m,点F(0,1)与点M(x,y)的距离为n.
(1)求圆C的圆心轨迹L的方程.
(2)求满足条件m=n的点M的轨迹Q的方程.
(3)在(2)的条件下,试探究轨迹Q上是否存在点B(x1,y1),使得过点B的切线与两坐标轴围成的三角形的面积等于
.若存在,请求出点B的坐标;若不存在,请说明理由.
如图，在正四棱锥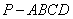
中，底面是边长为2的正方形，侧棱
,
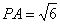为
的中点，
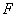是侧棱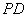
上的一动点。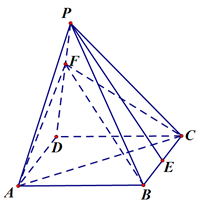
（1）证明：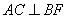
；
（2）当直线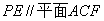
时，求三棱锥
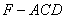的体积.
在一个盒子中，放有标号分别为
，
，
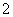的三个小球，现从这个盒子中，有放回地先后抽得两个小球的标号分别为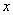
、
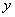，设
为坐标原点，设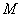
的坐标为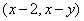
.
（1）求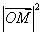
的所有取值之和；
（2）求事件“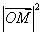取得最大值”的概率．
已知数列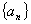
中，
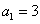，满足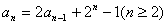
。
(1)求证：数列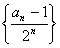
为等差数列;
(2)求数列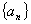的前
项和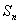
.
已知函数f(x)=lnx，g(x)=k·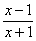
.
(I)求函数F(x)= f(x)- g(x)的单调区间；
(Ⅱ)当x>1时，函数f(x)> g(x)恒成立，求实数k的取值范围；
(Ⅲ)设正实数a1，a2，a3，，an满足a1+a2+a3++an=1，
求证：ln(1+
)+ln(1+
)++ln(1+
)>
．
数列{an}是公比为
的等比数列，且1-a2是a1与1+a3的等比中项，前n项和为Sn；数列{bn}是等差数列，b1=8，其前n项和Tn满足Tn=n
·bn+1(为常数，且≠1)．
(I)求数列{an}的通项公式及的值；
(Ⅱ)比较
+
+
++
与了Sn的大小．