已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
已知点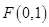 直线
直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线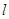 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)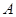 、
、 是轨迹
是轨迹 上异于坐标原点
上异于坐标原点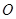 的不同两点,轨迹
的不同两点,轨迹 在点
在点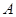 、
、 处的切线分别为
处的切线分别为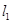 、
、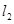 ,且
,且 ,
,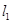 、
、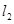 相交于点
相交于点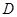 ,求点
,求点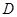 的纵坐标.
的纵坐标.
已知双曲线 的中心为原点
的中心为原点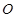 ,左、右焦点分别为
,左、右焦点分别为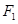 、
、 ,离心率为
,离心率为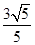 ,点
,点 是直线
是直线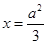 上任意一点,点
上任意一点,点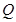 在双曲线
在双曲线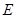 上,且满足
上,且满足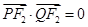 .
.
(1)求实数 的值;
的值;
(2)证明:直线 与直线
与直线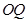 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为 ,过点
,过点 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、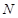 ,在线段
,在线段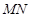 上去异于点
上去异于点 、
、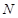 的点
的点 ,满足
,满足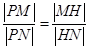 ,证明点
,证明点 恒在一条定直线上.
恒在一条定直线上.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,
且BC AE=DC
AE=DC AF,B、E、F、C四点共圆。
AF,B、E、F、C四点共圆。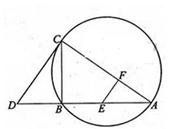
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值。
上海理)如图,已知曲线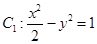 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与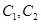 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明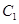 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证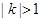 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
陕西理)已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(1) 求动圆圆心的轨迹C的方程;
(2) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P, Q, 若x轴是 的角平分线, 证明直线l过定点.
的角平分线, 证明直线l过定点.