已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
已知数列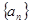 中,
中,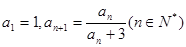
(1)求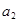 ,
,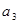 ;
;
(2)求证: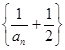 是等比数列,并求
是等比数列,并求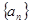 的通项公式
的通项公式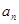 ;
;
(3)数列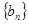 满足
满足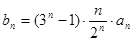 ,数列
,数列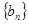 的前n项和为
的前n项和为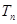 ,若不等式
,若不等式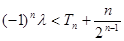 对一切
对一切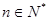 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.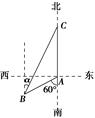
(1)求渔船甲的速度;
(2)求sinα的值.
已知数列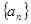 的前
的前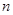 项和为
项和为 ,且2
,且2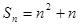 .
.
(1)求数列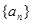 的通项公式;
的通项公式;
(2)若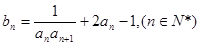 求数列
求数列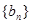 的前
的前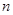 项和
项和 .
.
在△ABC中,a,b,c分别为角A,B,C的对边,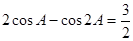
(1)求角A的度数;
(2)若a=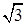 ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积.
在△ 中,角
中,角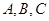 所对的边分别为
所对的边分别为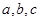 ,已知
,已知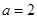 ,
,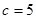 ,
,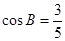 .
.
(1)求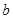 的值;
的值;
(2)求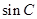 的值.
的值.