某人有甲、乙两个电子密码箱,欲存放A,B,C三份不同的重要文件,则两个密码箱都不空的概率是 .
下列表述中:
(1)若复数 满足
满足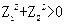 ,则
,则 ;
;
(2)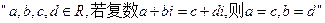 类比推出
类比推出 ,若
,若
(3)当 则
则 ;(4)线性回归方程
;(4)线性回归方程 中,当变量x平均增加一个单
中,当变量x平均增加一个单 位
位 时,
时, 平均增加0.1个单位。其中一定正确的语句是(填序号)。
平均增加0.1个单位。其中一定正确的语句是(填序号)。
若一组观测值(x1,y1)(x2,y2)…(xn,yn)之间满足yi=bxi+a+ei(i=1、2. …n)若ei恒为0,则R2为
.关于函数f(x)=4sin(2x+) (x∈R),有下列命题:
(1)y="f(x" )的表达式可改写为y="4cos" (2x — );(2)y="f(x" )是以2π为最小正周期的周期函数;(3)y=f(x)的图象关于点(— ,0)对称;(4)y=f(x)的图象关于直线
x= — 对称;其中正确的命题序号是________________________.
函数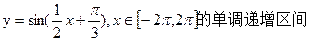 是________________;
是________________;
化简 = ____________________;
= ____________________;