为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
| 年龄 (岁) |
[15,25) |
[25,35) |
[35,45) |
[45,55) |
[55,65) |
[65,75] |
| 频 数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成 人数 |
4 |
8 |
9 |
6 |
4 |
3 |
(1)作出被调查人员年龄的频率分布直方图.
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
如图所示,在正方体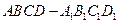 中,
中,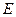 为
为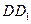 上的点、
上的点、 为
为 的中点.
的中点.
(Ⅰ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;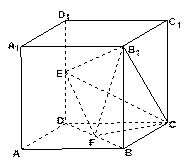 (Ⅱ)若直线
(Ⅱ)若直线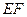 //平面
//平面 ,试确定点
,试确定点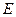 的位置.
的位置.
已知等差数列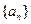 的前
的前 项和为
项和为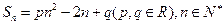
(I)求 的值;
的值;
(Ⅱ)若 ,数列
,数列 }满足
}满足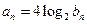 ,求数列
,求数列 的前
的前 项和.
项和.
在 中,角
中,角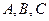 所对的边分别为
所对的边分别为 ,且
,且 .
.
(1)求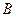 的大小;
的大小;
(2)若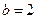 ,
, ,求
,求 的面积.
的面积.
选修4-4 :坐标系与参数方程
已知圆方程为 .
.
(1)求圆心轨迹的参数方程 ;
;
(2)点 是(1)中曲线
是(1)中曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围.
已知向量 ,动点
,动点 到定直线
到定直线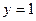 的距离等于
的距离等于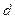 ,并且满足
,并且满足 ,其中
,其中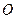 为坐标原点,
为坐标原点,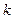 为非负实数.
为非负实数.
(1)求动点 的轨迹方程
的轨迹方程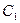 ;
;
(2)若将曲线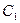 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(3)若(2)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足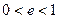 ,当
,当 是曲线
是曲线 的两个焦点时,则圆锥曲线上恒存在点
的两个焦点时,则圆锥曲线上恒存在点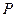 ,使得
,使得 成立,求实数
成立,求实数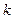 的取值范围.
的取值范围.