某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组 数 |
分 组 |
低碳族的人数 |
占本组的频率 |
| 第一组 |
[25,30) |
120 |
0.6 |
| 第二组 |
[30,35) |
195 |
p |
| 第三组 |
[35,40) |
100 |
0.5 |
| 第四组 |
[40,45) |
a |
0.4 |
| 第五组 |
[45,50) |
30 |
0.3 |
| 第六组 |
[50,55] |
15 |
0.3 |

(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=
| P(χ2≥x0) |
0.050 |
0.010 |
0.001 |
| x0 |
3.841 |
6.635 |
10.828 |
| 年龄组 是否低碳族 |
青 年 |
老 年 |
总 计 |
| 低碳族 |
|
|
|
| 非低碳族 |
|
|
|
| 总计 |
|
|
|
已知函数
(1)若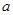 从集合{0,1,2,3}中任取一个元素,
从集合{0,1,2,3}中任取一个元素,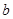 从集合{0,1,2}中任取一个元素,求方程
从集合{0,1,2}中任取一个元素,求方程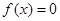 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若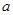 从区间[0,2]中任取一个数,
从区间[0,2]中任取一个数,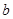 从区间[0,3]中任取一个数,求方程
从区间[0,3]中任取一个数,求方程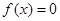 没有实根的概率.
没有实根的概率.
已知函数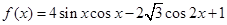 ,且给定条件
,且给定条件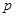 :“
:“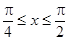 ”。
”。
(1)求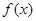 在给定条件
在给定条件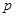 下的最大值及最小值;
下的最大值及最小值;
(2)若又给条件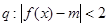 ,且
,且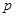 是
是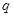 的充分不必要条件,求实数
的充分不必要条件,求实数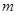 的取值范围。
的取值范围。
为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的1000名学生中抽出60名学生,将其成绩(成绩均为整数)分成六段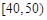 ,
,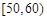 ,…,
,…,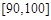 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: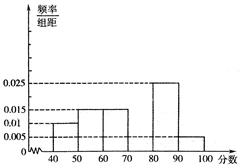
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的平均分和参加这次考试75分以上的人数;
已知命题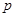 :函数
:函数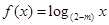 在
在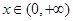 为减函数,命题
为减函数,命题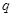 :函数
:函数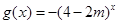 在R上为减函数,若命题
在R上为减函数,若命题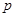 或
或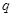 为真命题,命题
为真命题,命题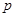 且
且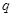 为假命题,求实数
为假命题,求实数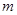 的取值范围.
的取值范围.
(本题12分)直线l:y=kx+1与双曲线C: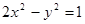 的右支交于不同的两点A,B
的右支交于不同的两点A,B
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.