质量为10 kg的物体按照s(t)=3t2+t+4的规律做直线运动,
求运动开始后4秒时物体的动能.
(本小题共12分) 已知两圆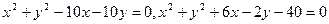 ,
,
求(1)它们的公共弦所在直线的方程;(2)公共弦长。
(本小题共12分) 证明函数 在
在 上是增函数。
上是增函数。
(本小题共12分)对于二次函数 ,
,
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)求函数的最大值或最小值;
(3)分析函数的单调性。
椭圆E经过点A(2,3),对称轴为坐标轴,焦点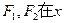 轴上,离心率
轴上,离心率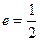
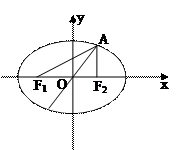
(I)求椭圆E的方程;
(II)求 的角平分线所在直线的方程
的角平分线所在直线的方程
围 建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)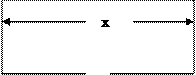
(I)将y表示为x的函数;
(II)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用