已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
设直线 的参数方程为
的参数方程为 (
( 为参数,
为参数, 为倾斜角),圆
为倾斜角),圆 的参数方程为
的参数方程为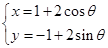 (
( 为参数).
为参数).
(1)若直线 经过圆
经过圆 的圆心,求直线
的圆心,求直线 的斜率.
的斜率.
(2)若直线 与圆
与圆 交于两个不同的点,求直线
交于两个不同的点,求直线 的斜率的取值范围.
的斜率的取值范围.
甲、乙两人各进行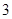 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为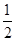 ,乙每次击中目标的概率为
,乙每次击中目标的概率为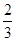 .
.
(1)求乙至多击中目标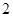 次的概率;
次的概率;
(2)记甲击中目标的次数为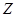 ,求
,求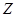 的分布列、数学期望和标准差.
的分布列、数学期望和标准差.
为了解某班学生喜爱打篮球是否与性别有关,对本班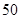 人进行了问卷调查得到了如下列表:
人进行了问卷调查得到了如下列表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
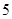 |
||
| 女生 |
 |
||
| 合计 |
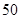 |
已知在全班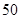 人中随机抽取
人中随机抽取 人,抽到喜爱打篮球的学生的概率为
人,抽到喜爱打篮球的学生的概率为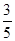 .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有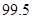 ﹪的把握认为喜爱打篮球与性别有关?说明你的理由.
﹪的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
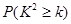 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
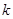 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: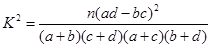 ,其中
,其中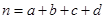 )
)
已知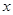 ,
,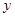 满足
满足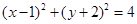 ,求
,求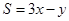 的最值.
的最值.
已知函数 .
.
(1)解不等式:  ;
;
(2)当 时, 不等式
时, 不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.