椭圆C: =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为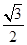 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1,PF2的斜率分别为k1,k2.若k≠0,试证明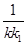 +
+ 为定值,并求出这个定值.
为定值,并求出这个定值.
某市举行青年教师数学解题大赛,从中随机抽取30名老师,将他们的竞赛成绩(满分100分,成绩均为不低于30分的整数)分成六段: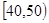 ,
,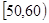 , ,
, ,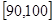 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.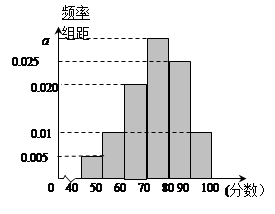
(Ⅰ)在这30名老师中随机抽取3名老师.求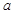 的值,以及同时满足下列两个条件的概率:①有且仅有1名老师成绩不低于90分;②成绩在
的值,以及同时满足下列两个条件的概率:①有且仅有1名老师成绩不低于90分;②成绩在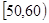 内至多1名老师;
内至多1名老师;
(Ⅱ)在成绩在 内的老师中随机抽取3名老师进行诊断调查,设成绩在
内的老师中随机抽取3名老师进行诊断调查,设成绩在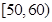 内的人数为随机变量
内的人数为随机变量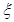 ,求
,求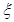 的分布列及其期望.
的分布列及其期望.
在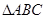 中,内角
中,内角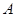 、
、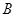 、
、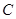 所对的边分别为
所对的边分别为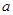 ,
,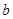 ,
,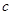 ,
,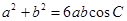 ,且
,且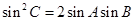 .
.
(Ⅰ)求角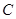 的值;
的值;
(Ⅱ)若点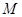 是
是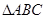 中角
中角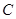 的外角内的一点,且
的外角内的一点,且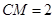 ,过点
,过点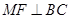 ,
,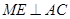 ,垂足分别为
,垂足分别为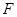 ,
,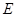 .求
.求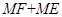 的最大值.
的最大值.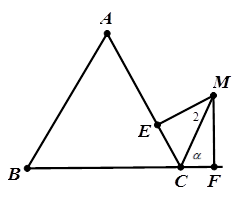
(本小题满分10分)选修4—5:不等式选讲
(Ⅰ)若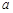 ,
,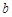 ,均为正数,且
,均为正数,且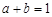 .证明:
.证明: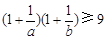 ;
;
(Ⅱ)设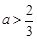 ,且
,且 时,
时,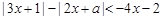 ,求实数
,求实数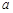 的取值范围.
的取值范围.
选修4—4坐标系与参数方程
在直角坐标系中,以坐标原点为极点,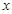 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为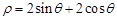 ,曲线D的参数方程为
,曲线D的参数方程为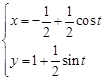 (
(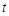 为参数).
为参数).
(Ⅰ)把C的极坐标方程化为直角坐标方程;
(Ⅱ)判定曲线C与曲线D间的位置关系.
选修4—1几何证明选讲
已知P是圆O外一点,PE切圆O于点E,A是圆O上一点,PA交圆O于B点,C为AE一点,PC交BE与D,CE=DE.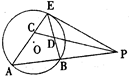
(Ⅰ)求证:PC是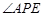 的平分线
的平分线
(Ⅱ)